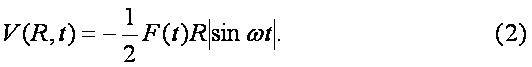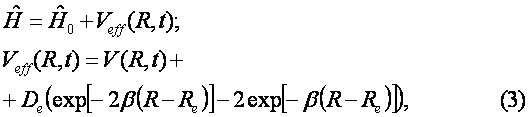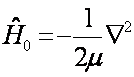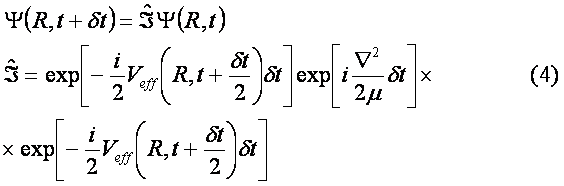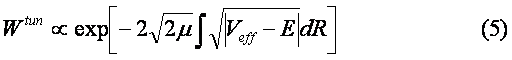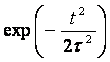Dissociation of benzene molecule in a strong low-frequency linearly polarized laser field is considered theoretically under the conditions of recent experiments. Analogy with the dissociation of diatomic molecules has been found. The dissociation probability of benzene molecule has been derived as a function of time. The three-photon dissociate process is shown to be realized in experiments.

Introduction.

The number of articles devoted to the interaction of molecules with a strong laser field increased considerably in recent years. The main features of interaction between diatomic molecules and a laser radiation were considered in a great number of experimental [1-5] and theoretical [6-9] papers. Classical and quantum investigations of spatial alignment of diatomic molecules and their molecular ions in a strong laser field, as well as ionization and dissociation of these molecules and their molecular ions account for physical pictures of all processes.

However, when considering complex organic molecules, we observe physical phenomena to be richer, and they are not thoroughly investigated. Most of results obtained for diatomic molecules can be generalized to the multi-atomic molecules. This short paper contains the results of theoretical derivations for dissociation of benzene molecule C6H6 in the field of linearly polarized Ti:Sapphire laser. Data were taken from experimental results by Chin’s group, Ref. [4]. We use the atomic system of units throughout the paper.

Theoretical approach.

Let us consider the benzene molecule C6H6 in the field of Ti:Sapphire laser with the wavelength l=400 nm, pulse length t=300 fs and maximum intensity Imax=2´1014 W/cm2. According to Ref. [4] first electron is ejected from this neutral molecule and then the dissociation of C6H6+-ion occurs.

The most probable channel for decay of this ion is the separation into the equal parts :

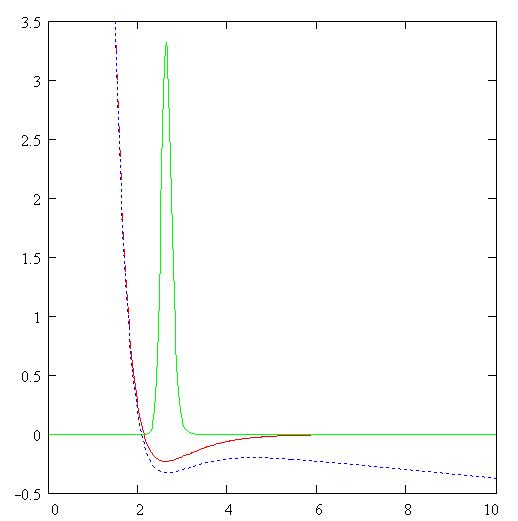
Of course, there is another channel for decay of C6H6+-ion which includes the ejection of the second electron and subsequent Coulomb explosion of the C6H6++-ion. We do not consider the latter process.

The channel (1) is seen to be similar to the dissociation of the hydrogen molecular ion considered in Ref. [2]. Indeed, the model scheme of energy levels for C6H6+-ion (see Ref. [4]) reminds the model scheme of energy levels for H2+ [2] containing only two low-lying electronic levels: 1sg (even) and 1su (odd).

Therefore we consider the dissociation process of C6H6+-ion analogously to that for H2+-ion (see Fig. 1). The benzene molecular ion has the large reduced mass with respect to division into equal parts. Hence, its wave function is well localized in space (see Fig. 2) and therefore we can apply classical mechanics for description of the dissociation process (1). However, the solution of Newton equation with the effective potential (see below) does not produce any dissociation, since laser pulse length is too small for such large inertial system. In addition to, effective potential barrier exists during the whole laser pulse and tunneling of the molecular fragment is impossible due to its large mass ( see Fig. 2). Thus, we should solve the dissociation problem in the frames of quantum mechanics.

The ground even electronic term of C6H6+-ion is presented here in the form of the well-known Morse potential with parameters b=2k and De=6.2 эВ, where k is approximated by the elastic constant of C-C coupling in the C6H6-molecule and De is the dissociation potential for the C2-molecule. The interaction of the molecular ion with the laser field is given by expression (see. Ref. [9])

Where the strength envelope of the laser radiation is chosen in the simple Gaussian form F(t)=F0exp(-t2/2t2) and R internuclear separation between the fragments C3H3+ and C3H3, w is the laser frequency and t is the laser pulse length. The value½sinwt½ takes into account the repulsion between the involved ground even electronic term and the first excited odd repulsive electronic term.

Thus, the Hamiltonian of the concerned system is

The kinetic energy operator being of the form

Where Re is the equilibrium internuclear separation. When calculating we make use of Re=1.39 A.

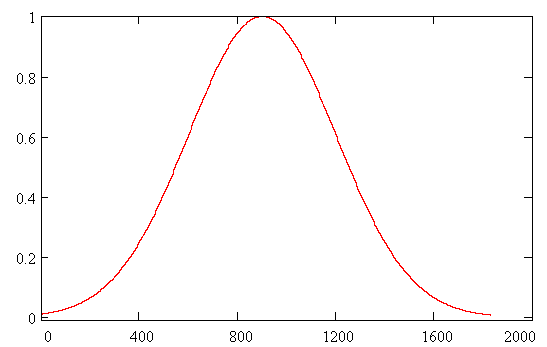
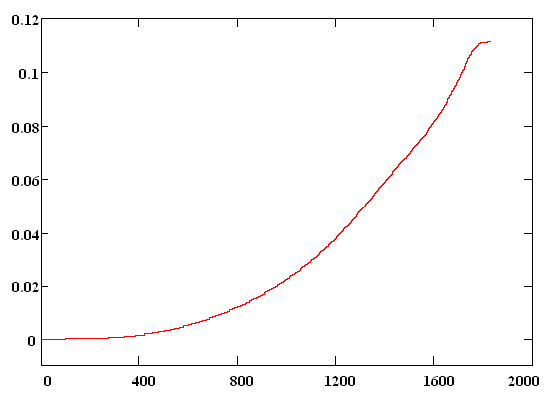
The time dependent Schrodinger equation with Hamiltonian (3) has been solved numerically by the split-operator method. The wave function has been derived by the iteration procedure according to formula

The initial wave function Y(R,0) was chosen as the solution of the unperturbed problem for a particle in the ground state of Morse potential.

The dissociation probability has been derived as a function of time according to formula W(t)=|<Y(R,0)|Y(R,t)>|2 . In Fig. 3 envelope of laser pulse is depicted and the dissociation probability W(t) is shown in Fig. 4.

Results.

The quantity W(t) is seen from Fig. 4 increase exponentially with time and it is equal to 0.11 after the end of laser pulse. It should be noted that the dissociation process can not be considered as a tunneling of a fragment through the effective potential barrier (see Fi. 2). Indeed, the
tunneling probability is on the order of magnitude of

Where Veff is substituted for maximum value of the field strength and the integral is derived over the classically forbidden region under the effective potential barrier. The tunneling effect is seen to be negligibly small due to large reduced mass of the molecular fragment m>>1. The Keldysh parameter g=w(2mE)1/2/F>>1. Thus, the dissociation is the pure multiphoton process. The frequency of laser field is w µ 2.7 эВ, while the dissociation potential is De=6 eV. Hence, three-photon process of dissociation takes place. The dissociation rate of three-photon process is proportional to m-1/2. The total dissociation probability is obtained by means of multiplying of this rate by the pulse length t. Therefore the probability of three-photon process can be large, unlike the tunneling probability. This is the explanation of large dissociation probability W»0.11 obtained in the calculations.

Conclusions.

Derivations given above of dissociation of benzene molecule show that approximately 11% of all C3H3+-ions decay on fragments C3H3 and C3H3+ under the conditions of Ref. [4]. The absorption of three photons occurs in this process.

Author is grateful to N. B. Delone, V. P. Krainov, M. V. Fedorov and S. P. Goreslavsky for stimulating discussions of this problem. This work was supported by Russian Foundation Investigations (grant N 96-02-18299).

Список литературы

Peter Dietrich, Donna T. Strickland, Michel Laberge and Paul B. Corkum, Phys. Rev. A, 47, N3, 2305 (1993). M. Ivanov, T. Siedeman, P. Corkum, Phys. Rev. A, 54, N2, 1541 (1996).

F. A. Ilkov, T. D. G. Walsh, S. Turgeon and S. L. Chin, Phys. Rev. A, 51, N4, R2695 (1995). F. A. Ilkov, T. D. G. Walsh, S. Turgeon and S. L. Chin, Chem. Phys. Lett 247 (1995).

S. L. Chin, Y. Liang, J. E. Decker, F. A. Ilkov, M. V. Amosov, J. Phys. B: At. Mol. Opt. Phys. 25 (1992), L249.

A. Talebpour, S. Larochelle and S. L. Chin, in press.

D. Normand, S. Dobosz, M. Lezius, P. D’Oliveira and M. Schmidt: in Multiphoton Processes, 1996, Conf., Garmish-Partenkirchen, Germany, Inst. Phys. Ser. No 154 (IOPP, Bristol 1997), p. 287.

A. Giusti-Suzor, F. H. Mies, L. F. DiMauro, E. Charon and B. Yang, J. Phys. B: At. Mol. Opt. Phys. 28 (1995) 309-339.

P. Dietrich, M. Yu. Ivanov, F. A. Ilkov and P. B. Corkum, Phys. Rev. Lett. 76, 1996.

S. Chelkowski, Tao Zuo, A. D. Bandrauk, Phys. Rev. A, 46, N9, R5342 (1992)

M. E. Sukharev, V. P. Krainov, JETP, 83, 457,1996. M. E. Sukharev, V. P. Krainov, Laser Physics, 7, No3, 803, 1997. M. E. Sukharev, V. P. Krainov, JETP, 113, No2, 573, 1998. M. E. Sukharev, V. P. Krainov, JOSA B, in press.

Figure captions

Fig. 1. Scheme of dissociation for benzene molecular ion C6H6+.

Fig. 2. The Morse potential (a), the effective potential (b) for maximum value of the field strength (a.u.), and the square of the wave function of the ground state for benzene molecular ion (c) as functions of the nuclear separation R (a.u.) between the fragments C3H3 and C3H3+.

Fig. 3. Envelope of laser pulse as a function of time (fs).

Fig. 4. The dissociation probability of benzene molecular ion C6H6+ as a function of time (fs).

Fig. 1

Morse potential (a) (a.u.),

effective potential for max. field (b) (a.u),

square of the wave function of the ground state for benzene molecular ion (c)

R, a.u.

Fig. 2

t, fs

Fig. 3


	b

W(t)

t, fs

Fig. 4

Для подготовки данной работы были использованы материалы с сайта http://mathematics.superreferat.ru