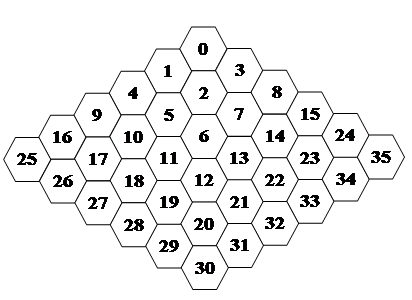
НЧР оказался столь остроумно устроен, что автору видится за этой конструкцией улыбающееся лицо Инженера, ведь остроумие присуще интеллекту, а никак не «первичной» бессознательной материи. Вначале была Программа.

“Ужель та самая” Программа? Ещё нет, это неправильная коническая развёртка натурального числового ряда. Неправильная, потому что её нельзя свернуть в конус, так чтобы числовые строки соединились в единую числовую спираль без зазоров или нахлёстов. Не позволяют это сделать квадратные ячейки, в которых мы расположили числовой ряд. Свернуть числовой ряд в конус можно только в том случае, если его ячейки будут правильными шестиугольниками.

Рис.13

И так далее.

Получившаяся сотовая структура представляет из себя правильную коническую развертку спирали НЧР, сохранившую все закономерности предыдущей развёртки. При сворачивании развёртки в конус, мы как бы застёгиваем её на молнию, стягивающую числовую ось квадратов N*N - 1, 4, 9, 16… с числовой осью N*(N+2) - 3, 8, 15, 24…

Шестигранные ячейки без изъянов прилегают друг к другу.

Если вместо чисел вы проставите в ячейках цифровые корни тех же чисел, то развертка проявит себя как решето для отсева простых чисел. «Зри в корень!» Цифровым корнем числа называется сумма всех его цифр. Суммируем, пока в ответе не останется одна цифра. Обычно цифровыми корнями пользуются нумерологи для определения чисел имени, рождения и т. д. Однако это вполне математический инструмент, используемый, например, для определения делимости чисел на 3 и 9.

Известен способ отыскания простых чисел в линейном числовом ряду. Это «решето Эратосфена», названное так по имени открывшего его великого математика. В сотовой таблице проявляются особые оси, на которых простыми числами будут те числа, сумма цифр которых будет либо только 2, либо только 5, либо только 8. Числа с другими цифровыми корнями, лежащие на этих осях, простыми быть не могут. Составные числа, лежащие на этих осях, будут либо кратны трём, либо иметь тот же цифровой корень, что и простые числа этой оси.

Пересекаясь между собой, оси строят «решето» на плоскости конической развёртки.. В узлах этого «решета» всегда находятся числа, которые делятся на 3. Если провести дополнительно оси типа N*(N+M) и оси чётных столбцов (каждый второй столбец), то в точках пересечения любых двух осей окажутся числа кратные трём. Таблица сама высекает все числа кратные двум и трём, а оси типа N*(N+M) вообще отсеивают все составные числа. В столбцах нечётных чисел остаются невычеркнутыми только простые. Сотовая таблица с двоичным приращением строки это уже «полноценное» двумерное решето для отсеивания простых чисел.

«Решето» для отсеивания чисел с цифровыми корнями 1, 4, и 7 проявляется в таблицах НЧР с квадратными ячейками и приращением числовой строки на 4 числа. Таким образом, можно считать понятие « цифровой корень» реабилитированным в глазах математиков, считающих нумерологию лженаукой. Вот такие «чудеса в решете», в сотовом решете.

Число характеризуется его величиной, а не линейными размерами, поэтому размеры числовой ячейки могут быть любыми.

Изменяя размеры числовой сотовой ячейки от бесконечно малых до бесконечно больших, мы получим бесконечное число конусов-матрёшек, вложенных друг в друга. Это не пустой кулёк из- под семечек, который можно смять и выбросить!

Сотовая ячейка каждой такой матрёшки это сечение шестигранной пирамиды. Пирамиды, растущие из оси числового конуса, укладываясь друг на друга, построили геометрически числовую модель пространства. Ось конуса это и есть натуральный числовой ряд в привычном прямолинейном виде. В зависимости от того, в каком масштабе вы будете укладывать числа, ось может быть и бесконечно малой точкой, и бесконечно длинной прямой. Соответственно и числовой конус изменяет свой объём от бесконечно малого до бесконечно большого. И потому «…в каждой точке Мир, весь Мир сосредоточен». А.Л. Чижевский.

Предлагаемая модель не требует поддержки математического аппарата, поскольку она уже включает его в себя. Она сама и есть этот математический аппарат!

Число — точка это ноль измерений.

Числовая ось — одно измерение.

Числовая развёртка — два измерения.

Числовой конус — три измерения.

Бесконечно растущий конус — три измерения + время!?

Как видно из вышеизложенного, математика — это не просто язык физики, это сама физика. Спиральное расположение НЧР я начал исследовать 10 февраля 1995 г. Осенью того же года познакомился с книгой «След на воде» В.Д. Плыкина, а вскоре и с самим учёным из Ижевска. Виктор Дмитриевич давно убеждён в первичности информации, а значит в существовании Программы. Им экспериментально обнаружено подтверждение сотового строения воды.

В книге Ю.Я. Светлакова, автора известной в Кузбассе телепередачи «Шаг за горизонт», я прочел о практическом исследовании новосибирского учёного В.С. Гребенникова. Цитирую: «Около многоячеистых гнёзд подземных пчёл он обнаружил странное, неизвестное науке волновое поле. Оказалось, что если в многоячеистом предмете, многослойном, многопористом, ритмически расположить отдельные элементы, ячейки, трубки, то он способен непонятным образом воздействовать на живые системы, организмы, в том числе и на человеческий». Виктор Степанович назвал это эффектом полостных структур. Становится очевидным, что сотовый конус это не умозрительная игрушка, а вездесущая реальность. Перейдём теперь к заявленной в названии работы религии.

«Пришёл я в сад мой, сестра моя, невеста; набрал мирры моей с ароматами моими, поел сотов моих с мёдом моим, напился вина моего с молоком моим. Ешьте, друзья; пейте и насыщайтесь, возлюбленные». Библия, Песнь Песней, глава 5.1.

«Нашёл ты мёд?» Там же, Притчи Соломона.

Когда Аполлон строил в Дельфах свой первый храм, пчёлы принесли ему из Гипербореи восковой образец и держали его на своих крыльях во всё время строительства. Стоит ли объяснять, что эта парящая в воздухе конструкция могла быть только сотовой? См. «Мифы Древней Греции» Ф. Зелинский.

Во многих книгах об античной культуре публикуется изображение статуи богини плодородия Деметры. Она выполнена в виде расширяющегося кверху конуса, а плечи Богини окутывает роскошный воротник из пчёл.

Храм Соломона выглядит как конус, перевёрнутый вершиной вниз, восходят в него по спиральной лестнице. В реальной жизни такое здание не может устоять, а значит, речь идёт о коническом Храме Мироздания! См. Библия, 3 Книга Царств, Глава 6.6. При этом в 1-й книге Паралипоменон, глава 28 сообщается, что чертежи дома Божия «в письмени от Господа»!

Храм, явившийся Иезекиилю в видении, тоже выглядит как расширяющийся кверху конус. См. Библия, Иезекииль, Глава 41. Этот храм снизу доверху, снаружи и изнутри расписан изображениями поочерёдно стоящих херувимов и пальм. Очевидно, это эзотерический намёк на стилизованное изображение сот.

За изобретение чисел боги наградили рогом изобилия Прометея, чьё имя означает «предвидящий». Числовой конус таковым рогом и является не только по геометрической форме, но и потому что содержит в себе всеобъемлющий математический аппарат. Откройте подходящий случаю закон, упакованный в показанной выше сотовой модели и материализуйте хоть манну небесную!

Однако будьте осторожны. Младшему брату титана Эпиметею, что значит «крепкий задним умом», боги подсунули полный бедствий и болезней ящик Пандорры. Эзотерика Священных Писаний мировых религий это fool proof, «защита от дурака», от преждевременного проникновения незрелой цивилизации в тайны Мироздания. Рог изобилия становится ящиком Падорры в руках невежд.

В последние годы по каналам ЦТ неоднократно демонстрировался документальный фильм об испытании советской термоядерной бомбы мощностью 50 мегатонн в тротиловом эквиваленте. При этом заметно как из под шапки термоядерного гриба вырастает правильный конус. Угол при вершине этого конуса на глаз совпадает с углом при вершине сотового конуса. Возможно, при таких взрывах проявляется обычно невидимая структура пространства.

До того как евреи начали строить храмы, их святилищем была скиния — шатёр. Обратимся теперь к Новому Завету.

Откровение, глава 15. 5: «…и вот отверзся храм скинии свидетельства на небе».

Послание Павла евреям, глава 9: «Но Христос, Первосвященник будущих благ, пришёл с большею и совершеннейшею скинией, нерукотворённою, то есть, не такового устроения».

И далее в той же главе: «Христос вошел не в рукотворённое святилище, по образу истинного устроенное (!), но в самоё небо».

Священное Писание Христианства открытым текстом сообщает нам, что Господь рассказывал ученикам о нерукотворном конусе, образе неба! И не его ли модель имел в виду Господь, когда говорил: «Разрушьте храм сей, и Я в три дня восстановлю его»? «Попасть пальцем в небо» не всегда значит ошибиться.

Прометей, Тантал, Иисус распяты по одной и той же причине – преждевременно открывали людям тайны неба, тайны богов. А судьи кто? Жрецы, конечно. Про них говорит Христос: «Горе вам, книжники и фарисеи, лицемеры, что затворяете Царство Небесное человекам; ибо сами не входите и хотящих войти не допускаете». От Матфея 23.13. «Горе вам, законникам, что вы взяли ключ разумения: сами не вошли и входящим воспрепятствовали». От Луки 11.52.

Не этих ли законников и фарисеев имели в виду Великие Посвящённые, когда писали один — «Собаку на сене», а другой «Скупого рыцаря»? То же самое в Коране, сура 3.64: «О, обладатели писания! Почему вы облекаете истину ложью и скрываете истину, в то время как вы знаете?».

Современным учёным лишь с недавних пор известно, что метагалактика имеет сотовое строение. Тот самый случай, когда новое — это хорошо забытое старое.

Православные священники носят головные уборы в форме опрокинутого усечённого конуса.

Колпак астролога — это конус, разрисованный звёздами. В таких колпачках американцы поздравляют друг друга с днём рождения

В Москве в историческом музее хранится бронзовая фигурка древнего Божества со спиралью на груди, сидящего верхом на волке. Она найдена на территории России, в Прикамье (в Гиперборее?). Иллюстрация из книги В.Н. Дёмина «Тайны русского народа».

Рис.14

В Мюнхенском музее хранится модель древнего храма, состоящая из шести(!) конусов(!), украшенных спиралями(!). Иллюстрация из книги В.Н. Дёмина «Тайны русского народа».

Рис.15

Змея издревле считается символом мудрости, потому что может сворачиваться спиралью и на коже её чётко прорисованы соты.

Другой символ мудрости, кадуцей, выглядит как конус, осью которого является вытянутая змея, спирально обвитая двумя другими змеями.

Накладные бородки у статуй фараонов - это всегда конус, сплетённый из перекрещивающихся спиралей. Непременным атрибутом этих статуй является урей, священная кобра, нависающая надо лбом фараона.

Великая пирамида в Гизе изначально была облицована шестигранными известняковыми плитами. Венцом её был ныне утраченный священный конус Бен-Бен. Опять соты и конус!

Один из символов у масонов – глаз, расположенный в треугольнике. Но ведь это едва замаскированная проекция конуса и его поперечного сечения.

Журнал «Наука и религия» описывает старинный перстень с изображением конуса, обвитого спиралью. Называется этот символ «знаком Мироздания»!

Пожалуй, достаточно примеров, подтверждающих, что на Земле существовали цивилизации, продвинувшиеся в познании законов Творца дальше нас. Они знали Истину. Ныне осколки этой Истины сохранились в Священных Писаниях различных религий и мифах древних народов.

Можно ли считать геометрически-числовой конус реализованной Программой Творца по организации пространства? “Думайте сами, решайте сами”. Те же Священные Писания утверждают, что и живая материя сотворена, в том числе и человек, по образу и подобию Божьему. Но об этом в следующей главе, которую воинствующим материалистам, ортодоксам от науки и фанатикам от религии лучше не читать.

ГЛАВА 2. Древо Познания

Попробуем найти вторую часть Программы, для живой природы. А это значит, что придется вновь обратиться к математике.

Каждому из нас со школы известно, что натуральный числовой ряд состоит из простых и составных чисел. Простые числа это те, которые делятся без остатка только сами на себя и на единицу.

Закон распределения простых чисел в НЧР математики ищут давно, но безуспешно. Эратосфен Александрийский, П. Ферма, Л. Эйлер, российский академик П.Л. Чебышев не нашли единой формулы для этого закона. Скорее всего потому, что он не имеет формального воплощения. Необходимо применить другой подход к проблеме.

Попробуем рассмотреть, как ведут себя простые числа, эти “неформалы”, в конических развертках, подобных вышеописанной.

Вернитесь к Рис.1, оставьте в нём на своих местах только простые числа, обозначив их для большей наглядности одинаковыми значками вместо цифр. Составные числа не проставляйте, пусть их ячейки останутся пустыми. Вы получите следующую картинку:

Рис.16

О

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19